|
بسم الله الرحمن الرحيم

إذا استخدمت
الكمبيوتر لأكثر من خمس دقائق فإنك - بالتأكيد - قد سمعت بكلمتي البت
Bit و البايت Byte،
فهما عبارة عن وحدتي فياس. كل من الـ RAM و
الأقراص الصلبة Hard Disks تقاس سعتها بالـByte.
و لا بد أنك
قد قرأت عر وضاً أو إعلانات من قبل تقول ((
هذا الكمبيوتر يحتوي على معالج بنتيوم Pintium
32-bit و 512 ميجابايت
Megabyte من ذاكرة RAM
و Hard Disk سعته 80 جيجابايت
Gigabyte )).
سنتعرف في
هذا الموضوع على الـ Bit و الـ
Byte بشكل أعمق و لكن قبل
البدء أريد أن أشير إلى الرق بين كلمتي رقم digit
و عدد number، فالرقم يتشكل من خانة واحدة
بينما يتشكل العدد من عدة أرقام: و في النظام العشري فإن 0 و 1 و 2 .. 9
تشكل جميعها أرقام بينما 6473 يعتبر عدداً.
 نظام الأرقام العشري Decimal Number System
نظام الأرقام العشري Decimal Number System
جميعنا يعرف نظام
الأرقام العشري و الذي يتكون من الأرقام من 0 إلى 9 و التي بواسطتها يمكن
تشكيل أي عدد. لنأخذ بعين الاعتبار العدد 6473؛ فهو يتشكل من أربعة أرقام
لكل رقم منها مرتبة، فالرقم 3 يشكل المرتبة رقم 0، و الرقم 7 يشكل
المرتبة رقم 1.. و بشكل عام فإن أي رقم يوجد في أي
عدد يحمل مرتبة تبدأ من الصفر في أول رقم في اليمين و تتزايد
قيمة المرتبة كلما اتجهنا لليسار.. العبرة من هذا هو أننا نستطيع التعبير
عن العدد بواسطة قوى العدد عشرة Powers of 10؛
فنقوم
بضرب كل رقم يشكل هذا العدد في العدد 10 مرفوع إلى أس يساوي مرتبة هذا
الرقم، أي:
|

( 6 * 10^3
) + ( 4 * 10^2 ) + ( 7 * 10^1
) + ( 3 * 10^0 ) = 6000 +
400 + 7 + 3 = 6473
لاحظ
أن الإشارة "^" تعبر عن القوة التي يرفع لها العدد الذي يقع على
يسارها |
إذن فهناك علاقة
وطيدة بين أي عدد في النظام العشري و بين العدد عشرة نفسه.. قد يتبادر
إلى ذهنك السؤال: لماذا نظام الأرقام لدينا يعتمد على عشرة أرقام - لماذا
ليست ثمانية مثلاً؟ في الحقيقة لا شيء يجبرنا على استخدام هذا النظام،
إلا أن النظام العشري مرتبط مع عدد أصابع اليد لذا نجده أكثر سهولة.. لكن
يمكننا بكل سهولة تطوير نظام أرقام يحتوي على ثمانية أرقام (( أي يكون
الرقم 8 هو الأساس في هذا النظام )).. بل يمكننا تطوير نظام أرقام يعتمد
على أي رقم كأساس!
 نظام الأرقام
الثنائي Binary number system - البت Bit
نظام الأرقام
الثنائي Binary number system - البت Bit
قد تتساءل لماذا يستخدم الكمبيوتر هذا
النظام و لا يستخدم النظام العشري؟ الجواب يكمن في التقنية الإلكترونية
التي بني عليها الحاسوب.
في
الحقيقة فإن أسهل طريقة لفهم النظام الثنائي هي مقارنته بالنظام العشري،
فهو يحتوي على رقمين فقط و هما 0 و 1 بواسطتهما يمكن تشكيل أي عدد ثنائي،
يسمى كل من هذين الرقمين بالـ Bit اختصاراً لـ (( BInary Digit - رقم
ثنائي ))، لذا فإننا سنستخدم الكلمة bit للتعبير عن إما 0 أو 1.. لنأخذ
بعين الاعتبار العدد الثنائي 1011، سنتبع نفس الطريقة التي اتبعناها مع
الرقم 6473 و لكن بما أن النظام الثنائي يعتمد على الرقم 2 فإن أساسه هو
العدد 2 بدلاَ من 10 في النظام العشري، و بهذه الطريقة نستطيع تحويل أي
عدد ثنائي إلى قيمته في النظام العشري:
|

( 1
* 2^3
) + ( 0 * 2^2
) + ( 1 * 2^1
) + ( 1 * 2^0
) = 8 + 0 + 2 + 1 = 11 |
كما تلاحظ فإن كل bit يحمل قيمة متزايدة
لقوى العدد 2، هذا ما يجعل العد في النظام الثنائي سهلاً، و سيكون شكل
الأعداد من 0 إلى 20 في النظام الثنائي كالتالي:
0 = 0
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 = 1001
10 = 1010
11 = 1011
12 = 1100
13 = 1101
14 = 1110
15 = 1111
16 = 10000
17 = 10001
18 = 10010
19 = 10011
20 = 10100
لاحظ أن العدد 0 في النظام العشري يمثله
العدد 0 في النظام الثنائي و نفس الحال مع العدد 1، و لكن العدد 2 يتمثل
باعدد 10 في النظام الثنائي! هذا يرجع إلى كون العدد 2 غير موجود بالنطام
الثنائي لذا فعندما نجمع 1 + 1 فالمجموع هو 0 و العدد في الخانة التالية
يحال إلى 1. أنظر إلى المثال التالي و الذي نجمع فيه العددين الثنائيين
11 + 110:
|
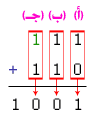
11
+ 110 = 1001
(
أ )
حاصل جمع 1 + 0 هو 1 بدون باقي.
(ب)
حاصل جمع 1 + 1 هو 0 و الباقي 1، نضيفه مع الخانة التالية.
(جـ) حاصل جمع 1 + 1 هو 0 و الباقي 1، نضيفه مع الخانة التالية لينتج في
الآخير 1. |
 البايت Byte البايت Byte
من النادر أن تجد الـ Bits وحيدة في
الكمبيوتر، بل هي دائماً تجمع مع بعضها على شكل مجموعات من 8-بت تسمى
بايت Byte. لماذا هنالك 8 بت في كل بايت؟ هذا السؤال مشابه تماماً للسؤال
"لماذا هنالك 12 بيضه في الدرزينة؟!" بعد إجراء عدة اختبارات و أخطاء في
الخمسين عاماً المنصرمة أتفق على جعل البايت يتشكل من 8 بت.
مع وجود 8 بت في البايت، يمكنك أن تحصل على
256 قيمة مختلفة تتدرج بين 0 إلى 255، كما في التالي:
0 = 00000000
1 = 00000001
2 = 00000010
...
254 = 11111110
255 = 11111111
أما إذا أخذنا في الاعتبار 2 بايت ( 16-بت
) فإننا سنتحصل على قيم بين 0 و 65,535 كالتالي:
0 = 0000000000000000
1 = 0000000000000001
2 = 0000000000000010
...
65534 = 1111111111111110
65535 = 1111111111111111
 Lots of Bytes Lots of Bytes
ما أن تبدأ الحديث عن البايت فإنك ستجد
نفسك أمام بادئات Prefixes مثل كيلو Kilo، ميجا Mega، جيجا Giga - أي
كيلوبايت kilobyte، ميجابايت megabyte و جيجابايت gigabyte و اختصاراتها
( ك.ب. KB، م.ب. MB، جـ.ب. GB )، و الجدول التالي يبين هذه البادئات و
قيمها بالنسبة للبايت الواحد:
|
الاسم |
اختصار |
الحجم بالبايت |
|
Kilo |
K |
2^10 = 1,024 |
|
Mega |
M |
2^20 = 1,048,576 |
|
Giga |
G |
2^30 = 1,073,741,824 |
|
Tera |
T |
2^40 = 1,099,511,627,776 |
|
Peta |
P |
2^50 =
1,125,899,906,842,624 |
|
Exa |
E |
2^60 =
1,152,921,504,606,846,976 |
|
Zetta |
Z |
2^70 =
1,180,591,620,717,411,303,424 |
|
Yotta |
Y |
2^80 =
1,208,925,819,614,629,174,706,176 |
على حسب هذا الجدول فإنه عندما يخبرك أحدهم
بأن جهازه يحتوي (( قرصاً صلباً Hard Disk سعته 2 جيجابايت Gigabyte ))
فهذا يعني أن القرص الصلب لديه يستطيع حفظ بيانات يصل حجمها إلى 2
جيجابايت Gigabyte أي تقريباً ملياري بايت من البيانات و تحديدا
2,147,483,648 بايت. قد تستغرب من كبر هذا الرقم و لكن إذا أخذت بعين
الاعتبار أن سعة الاسطوانة المضغوطة CD قد
تصل إلى 700 ميجابايت Megabyte
فإنك ستستنتج أن 3 اسطوانات من هذا النوع تكفي لتعبئة الأمر كله! و هنالك
قواعد بيانات Databases تعدى حجمها التترابايت Tetrabyte (( أي تقريباً
1000 جيجابايت Gigabyte ))، و هنالك بعض قواعد البيانات الي بلغت
عدة
بيتابايت Petabyte (( أي تقريباً مليون جيجابايت Gigabyte )) موجودة في
البنتاغون!
تحياتي؛
مازن الهجري
|